1.4 使用逻辑门实现布尔函数

在本教程中，我们将学习如何使用逻辑门实现布尔函数。在之前的教程中，我们学习了布尔代数定律及其相关定理。我们还了解到布尔函数可以方便地表示为与或表达式（SOP，Sum of Products）形式和或与表达式（POS，Product of Sums）形式。为了逻辑地表示这些标准化的方程，我们使用逻辑门。

任何布尔函数都可以通过适当连接多个逻辑门来表示。使用逻辑门实现布尔函数是一种非常简单且方便的形式。

通过使用逻辑门实现布尔函数，涉及将一个逻辑门的输出连接到另一个门的输入。常用的逻辑门包括：与门（AND）、或门（OR）、与非门（NAND）和或非门（NOR）。

接下来，我们来看一下布尔函数的 SOP 和 POS 形式的逻辑门实现。

逻辑门简介

逻辑门是数字电子电路的基本构建模块。逻辑门是一种电子电路，可用于实现布尔表达式。

布尔逻辑的定律和定理用于操作布尔表达式，而逻辑门则用于在数字电子学中实现这些布尔表达式。

与门（AND）、或门（OR）和非门（NOT）是数字电子学中使用的三种基本逻辑门。通过使用这些基本逻辑门，我们可以推导出其他逻辑门，如与非门（NAND）、或非门（NOR）、异或门（Exclusive OR，Ex-OR）和同或门（Exclusive NOR，Ex-NOR）。

在查看使用逻辑门实现布尔函数之前，让我们快速回顾一下关于重要逻辑门的一些基础知识。

与门（AND Gate）

逻辑与门是一种基本逻辑门，具有两个或多个输入和一个输出。只有当与门的所有输入均为高电平时，其输出才为高电平。在所有其他输入情况下，输出均为低电平。与门的逻辑符号和真值表如下所示。

A	B	$Y = A \cdot B$
0	0	0
0	1	0
1	0	0
1	1	1

如果 $A$ 和 $B$ 是与门的两个输入，则输出表达式可写为：

$Y = A \cdot B \quad \text{或} \quad Y = A \land B$

读作“Y 等于 A 与 B”。

或门（OR Gate）

或门用于执行逻辑“或”运算。或门也包含两个或多个输入和一个输出。如果或门的任意一个输入为高电平，则其输出为高电平。当所有输入均为低电平时，输出为低电平。或门的逻辑符号和真值表如下所示。

A	B	$Y = A + B$
0	0	0
0	1	1
1	0	1
1	1	1

如果 $A$ 和 $B$ 是或门的两个输入，则输出表达式可写为：

$Y = A + B$

读作“Y 等于 A 或 B”。

非门（NOT Gate）

逻辑非门是另一种基本逻辑门，具有一个输入和一个输出。非门的输出始终是输入的反相。如果输入为高电平，则输出为低电平；如果输入为低电平，则输出为高电平。非门的逻辑符号和真值表如下所示。

X	$Y = \overline{X}$
0	1
1	0

非门用于在布尔代数中产生变量的反相。因此，它也被称为反相器或补码电路。

使用逻辑门实现 SOP 布尔函数

与或表达式（SOP）形式通过使用基本逻辑门（与门和或门）来表示。SOP 形式的实现将在输入端使用与门，由于函数的输出是所有乘积项的和，因此在输出端使用或门。

需要记住的重要一点是，我们使用非门来表示变量的反相或补码。

与或表达式（SOP）

• 输入：与门
• 输出：或门

两个输入变量的实现

让我们了解如何使用基本逻辑门实现以下布尔函数。

$F = A \cdot B + A \cdot \overline{B}$

在给定的 SOP 函数中，我们有一个反相项 $\overline{B}$。因此，为了表示反相输入，我们在输入端使用非门。为了表示乘积项，我们使用与门。参见下面给出的逻辑图，用于表示布尔函数。

三个输入变量的实现

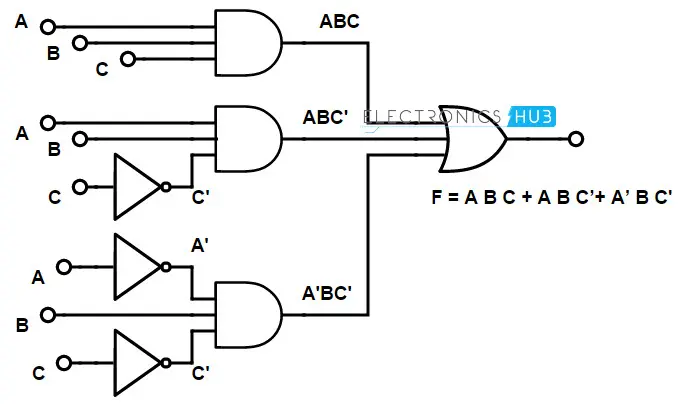
现在我们来看如何使用基本逻辑门实现以下布尔函数。这是一个包含三个输入变量的函数。

$F = A \cdot B \cdot C + \overline{A} \cdot \overline{B} \cdot C + A \cdot \overline{B} \cdot C$

在给定的函数中，我们有两个反相项 $\overline{A}$ 和 $\overline{C}$。因此，为了表示反相输入，我们在输入端使用非门。为了表示乘积项，我们使用与门。参见下面给出的逻辑图，用于表示布尔函数。

使用逻辑门实现 POS 布尔函数

或与表达式（POS）形式可以通过使用基本逻辑门（与门和或门）来表示。POS 形式的实现将在输入端使用或门，由于函数的输出是所有和项的乘积，因此在输出端使用与门。在 POS 形式的实现中，我们使用非门来表示变量的反相或补码。

或与表达式（POS）

• 输入：或门
• 输出：与门

两个输入变量的实现

现在我们来看如何使用基本逻辑门实现以下布尔函数。

$F = (A + B) \cdot (A + \overline{B})$

在给定的函数中，我们有一个反相项 $\overline{B}$。因此，为了表示反相输入，我们在输入端使用非门。为了表示和项，我们使用或门。参见下面的逻辑图，用于表示布尔函数。

三个输入变量的实现

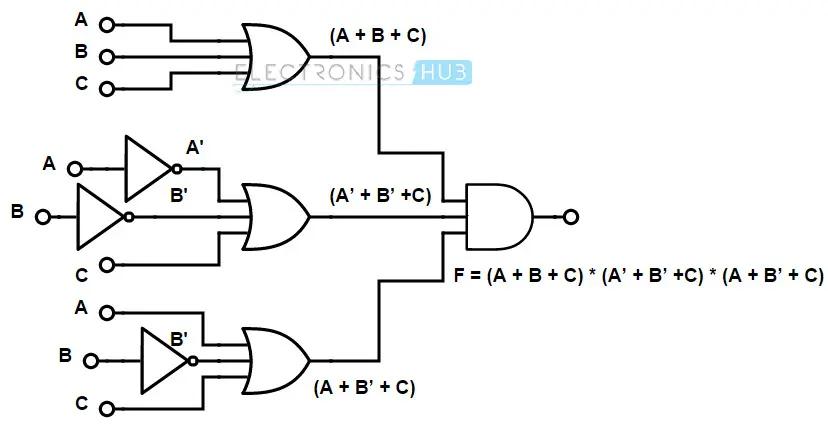
使用基本逻辑门实现布尔函数。

$F = (A + B + C) \cdot (A + \overline{B} + C) \cdot (A + B + \overline{C})$

在给定的布尔函数中，我们有两个反相项 $\overline{A}$ 和 $\overline{B}$。因此，为了表示反相输入，我们在输入端使用非门。为了表示和项，我们使用或门。参见下面给出的逻辑图，用于表示布尔函数。

使用通用逻辑门实现布尔函数

与非门（NAND）和或非门（NOR）被认为是“通用逻辑门”。原因在于，与非门和或非门可以执行（或可以像）所有三种基本门的功能，即与门、或门和非门。我们可以通过使用与非门或或非门来设计任何基本逻辑门。这就是为什么它们被称为“通用门”。

让我们看看如何使用通用逻辑门实现布尔函数。

使用与非门实现布尔函数

与非门是与门和非门的逻辑组合，它可以像与门、或门和非门一样工作。因此，我们使用与非门来实现布尔函数。

关于与非门需要记住的重要一点是，它是基本与门的反相。这意味着与非门的输出等于与门输出的补码。

让我们通过一个例子来了解实现过程。

使用与非逻辑门实现布尔函数。

$F(A, B, C, D, E) = A + (\overline{B} + C)(\overline{D} + B\overline{E})$

在与非门实现中，我们在输入端和输出端都使用与非门。观察下面设计的逻辑图。使用与非门实现给定布尔函数的逐步过程如下所示。

首先，应使用与或门表示给定的布尔函数或方程。与或实现如下所示。

为了将与门转换为与非门，在与门的输出端引入一个气泡（补码）。为了补偿气泡，在下一个门的输入端也引入一个气泡。实现如下所示。

为了在输入端保持一致性，如果一个门的一个输入有气泡，则另一个输入也引入一个气泡。再次，为了补偿气泡，在前一个门的输出端引入一个气泡或对字面量进行补码。如下图所示。

如果或门的任意输入端都没有气泡，则引入气泡并适当补偿，如下图所示。

根据德摩根定律（$\overline{A} + \overline{B} = \overline{A \cdot B}$），具有两个反相输入的或门等价于与非门。因此，将具有两个反相输入的或门替换为与非门后，我们得到了使用与非门实现布尔函数的最终结构。最终实现如下所示。

或非门是或门和非门的组合，它可以像与门、或门和非门一样工作。因此，我们使用或非门来实现布尔函数。需要记住的重要一点是，或非门是基本或门的反相。这意味着或非门的输出等于或门输出的补码。

让我们通过一个例子来了解实现过程。

使用或非逻辑门实现布尔函数。

$g(A, B, C, D, E, F) = (A \cdot E) + (B \cdot D \cdot E) + (B \cdot C \cdot E \cdot F)$

我们可以将上述方程重写为：

$g(A, B, C, D, E, F) = A \cdot E + B \cdot D \cdot E + B \cdot C \cdot E \cdot F$ $= (A + B \cdot D + B \cdot C \cdot F) \cdot E$ $= (A + B \cdot (D + C \cdot F)) \cdot E$

在或非门实现中，我们在输入端和输出端都使用或非门。观察下面设计的逻辑图。

结论

这是一个关于如何使用逻辑门实现布尔函数的完整初学者教程。你学习了逻辑门（与门、或门、非门）的基础知识，以及方程的与或表达式（SOP）和或与表达式（POS）表示形式及其使用逻辑门的实现，还有使用通用门（与非门和或非门）实现布尔表达式的方法。